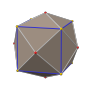
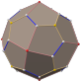
Truncated dodecahedron

Truncated dodecahedron
Type	Archimedean solid
Faces	32
Edges	90
Symmetry group	icosahedral symmetry $\mathrm {I} _{\mathrm {h} }$
Dihedral angle (degrees)	10-10: 116.57° 3-10: 142.62°
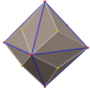
Dual polyhedron	Triakis icosahedron
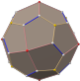
Vertex figure
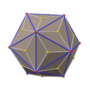
Net

In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.

Construction

The truncated dodecahedron is constructed from a regular dodecahedron by cutting all of its vertices off, a process known as truncation. This process of construction results in the pentagonal faces becoming decagonal faces, and the vertices become triangles. Therefore, it has 32 faces, 90 edges, and 60 vertices.

The truncated dodecahedron may also be constructed by using Cartesian coordinates. With an edge length $2\varphi -2$ centered at the origin, they are all even permutations of

$$\left(0,\pm {\frac {1}{\varphi }},\pm (2+\varphi )\right),\qquad \left(\pm {\frac {1}{\varphi }},\pm \varphi ,\pm 2\varphi \right),\qquad \left(\pm \varphi ,\pm 2,\pm (\varphi +1)\right),$$

where ${\textstyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$ is the golden ratio.

Properties

The surface area $A$ and the volume $V$ of a truncated dodecahedron of edge length $a$ are:

$${\begin{aligned}A&=5\left({\sqrt {3}}+6{\sqrt {5+2{\sqrt {5}}}}\right)a^{2}&&\approx 100.991a^{2}\\V&={\frac {5}{12}}\left(99+47{\sqrt {5}}\right)a^{3}&&\approx 85.040a^{3}\end{aligned}}$$

The dihedral angle of a truncated dodecahedron between two regular dodecahedral faces is 116.57°, and that between triangle-to-dodecahedron is 142.62°

3D model of a truncated dodecahedron

The truncated dodecahedron is an Archimedean solid, meaning it is a highly symmetric and semi-regular polyhedron, and two or more different regular polygonal faces meet in a vertex. It has the same symmetry as the regular icosahedron, the icosahedral symmetry. Its dual is triakis icosahedron, a Catalan solid, which shares the same symmetry as the truncated dodecahedron. It is non-chiral, meaning it is congruent to its own mirror image.

Truncated dodecahedral graph

Truncated dodecahedral graph
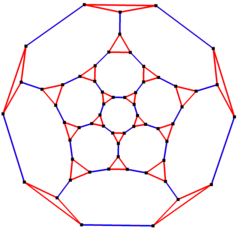5-fold symmetry Schlegel diagram
Vertices	60
Edges	90
Automorphisms	120
Chromatic number	3
Chromatic index	3
Properties	Cubic, Hamiltonian, regular, zero-symmetric
Table of graphs and parameters

In the mathematical field of graph theory, a truncated dodecahedral graph is the graph of vertices and edges of the truncated dodecahedron, one of the Archimedean solids. It has 60 vertices and 90 edges, and is a cubic Archimedean graph.

Circular

References

• Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.
• Diudea, M. V. (2018), Multi-shell Polyhedral Clusters, Springer, doi:10.1007/978-3-319-64123-2, ISBN 978-3-319-64123-2.
• Koca, M.; Koca, N. O. (2013), "Coxeter groups, quaternions, symmetries of polyhedra and 4D polytopes", Mathematical Physics: Proceedings of the 13th Regional Conference, Antalya, Turkey, 27–31 October 2010, World Scientific.
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
• Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.

External links

• Weisstein, Eric W., "Truncated dodecahedron" ("Archimedean solid") at MathWorld.
  • Weisstein, Eric W. "Truncated dodecahedral graph". MathWorld.
• Klitzing, Richard. "3D convex uniform polyhedra o3x5x - tid".
• Editable printable net of a truncated dodecahedron with interactive 3D view
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra